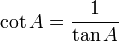Dari : Bani Biasa ( cuma itu yg inget ^^)
Rumus trigonometri untuk jumlah dan selisih sudut.

Rumus trigonometri untuk sudut rangkap (2a).
Sin 2 a = 2 Sin a . cos a
Sin 3 a = -4 Sin3 a + 3 Sin a
Cos 2 a = Cos2 a – Sin2 a
Cos 2 a = 1 – 2 Sin2 a
Cos 2 a = 2 Cos2 a – 1
Cos 3a = 4 Cos3 a – 3 Cos a


Rumus trigonometri sudut pertengahan (1/2 a).

Rumus trigonometri perkalian sinus dan cosinus.
2 Sin a Cos b = Sin (a+b) + Sin (a-b)
2 Cos a Sin b = Sin (a+b) – Sin (a-b)
2 Cos a Cos b = Cos (a+b) + Cos (a-b)
2 Sin a Sin b = – { Cos (a+b) – Cos (a-b) }
Rumus jumlah dan selisih trigonometri.

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Sinus
Sinus dalam matematika adalah perbandingan sisi segitiga yang ada di depan sudut dengan sisi miring (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi sinus di atas maka nilai sinus adalah

Nilai sinus positif di kuadran I dan II dan negatif di kuadran III dan IV.
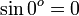



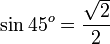

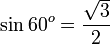
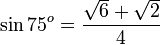

Kosinus
Kosinus atau cosinus (simbol: cos) dalam matematika adalah perbandingan sisi segitiga yang terletak di sudut dengan sisi miring (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan. Berdasarkan definisi kosinus di atas maka nilai kosinus adalah

Nilai kosinus positif di kuadran I dan IV dan negatif di kuadran II dan III.

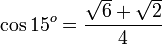
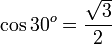

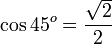


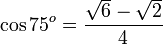

Tangen
Tangen (bahasa Belanda: tangens; lambang tg, tan) dalam matematika adalah perbandingan sisi segitiga yang ada di depan sudut dengan sisi segitiga yang terletak di sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi tangen di atas maka nilai tangen adalah

Nilai tangen positif di kuadran I dan III dan negatif di kuadran II dan IV.
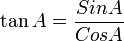







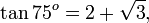

Sekan
Sekan (lambang: sec) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak pada sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi sekan di atas maka nilai sekan adalah

Hubungan sekan dengan kosinus:

Kosekan
Kosekan (disimbolkan dengan cosec atau csc) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi kosekan di atas maka nilai kosekan adalah

Hubungan kosekan dengan sinus:
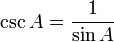
Kotangen
Kotangen (lambang: cot, cotg, atau cotan) dalam matematika adalah perbandingan sisi segitiga yang terletak pada sudut dengan sisi segitiga yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi kotangen di atas maka nilai kotangen adalah

Hubungan kotangen dengan tangen: